目标
- 定义三维向量(Vector3f)类,实现向量的常用计算方法。
- 扩展实现二维向量、四维向量。
源代码:
实现
三维向量
三维向量类的基本定义为:
public class Vector3f {
public float x, y, z;
public Vector3f() {
x = y = z = 0;
}
public Vector3f(float x, float y, float z) {
this.x = x;
this.y = y;
this.z = z;
}
}
Vector3f 可以用来表示三维空间中的一个“点”,这时 (x, y, z) 描述了该“点”在自身坐标系统中的相对位置。
Vector3f 也可以用来表示方向,看作是从原点 (0, 0, 0) 出发,指向 (x, y, z) 的箭头。这个“箭头”具有长度,也称为向量的模。
零向量
3D零向量表示为 (0, 0, 0),它是唯一一个长度为0的向量。
public final static Vector3f ZERO = new Vector3f(0, 0, 0);
负向量
把向量的各个分量求负,可得其负向量。简单地说就是 x + (-x) = 0。
负向量可以看作与原向量长度相同,但是方向相反的向量。
/**
* 求负向量
*
* @return
*/
public Vector3f negate() {
return new Vector3f(-x, -y, -z);
}
/**
* 求负向量
*
* @return
*/
public Vector3f negateLocal() {
x = -x;
y = -y;
z = -z;
return this;
}
注意,这里我学习 jMonkeyEngine 写了2个不同的实现。
- negate() 方法不会改变原向量,而是返回一个新的向量,它是原向量的负向量;
- negateLocal() 方法会改变原向量自身的值,并返回该向量本身。
在进行Java游戏开发时,应该尽量避免实例化新的对象,以减少GC的工作量。在下文出现的其它方法中,如果不做特别声明,名为 xxxLocal() 的方法都意味着不会返回新的对象,而是修改当前对象的值。
向量大小(长度或模)
计算向量各分量的平方和,然后开根号即可。
/**
* 返回向量的长度
*
* @return
*/
public float length() {
return (float) Math.sqrt(x * x + y * y + z * z);
}
开根号是一个相当昂贵的运算。如果只是想比较两个向量的大小,可以直接比较不开根号的值。若要判断向量长度是否为 1 或 0,也不需要开根号,因为1和0的平方等于它们本身。
所以,一般在3D数学库中,会提供这样一个方法,来返回未开根号的平方和:
/**
* 返回向量长度的平方
*
* @return
*/
public float lengthSquared() {
return x * x + y * y + z * z;
}
出于性能考虑,我并没有在 length() 方法中调用 lengthSquared() 方法,因为调用方法时虚拟机会创建栈帧、压栈、弹栈。虽然这些操作的时间很短暂,但是累积起来也会影响程序的性能。
在后面的方法中,如无必要,也会尽量减少方法的调用。
标量与向量的乘法
标量与向量的乘法非常直接,将向量的每个分量都与标量相乘即可。
/**
* 标量乘法
*
* @param scalor
* @return
*/
public Vector3f mult(float scalor) {
return new Vector3f(x * scalor, y * scalor, z * scalor);
}
/**
* 标量乘法
*
* @param scalor
* @return
*/
public Vector3f multLocal(float scalor) {
x *= scalor;
y *= scalor;
z *= scalor;
return this;
}
标准化向量
对于许多向量,我们只关心它的方向而不关心其大小。如:“我面向的是什么方向?”,这样的情况下使用单位向量更为简单。
单位向量就是长度为1的向量。单位向量经常也被称作标准化向量或更简单地称为 “法线”。
一般我会把与三个坐标轴平行的单位向量定义为常量。
public final static Vector3f UNIT_X = new Vector3f(1, 0, 0);
public final static Vector3f UNIT_Y = new Vector3f(0, 1, 0);
public final static Vector3f UNIT_Z = new Vector3f(0, 0, 1);
对于任意非零向量v,都可以计算出一个与它方向相同的单位向量。这个过程称作向量的“标准化”。要标准化向量,将向量除以它的大小(模)即可。
/**
* 求单位向量
*/
public Vector3f normalize() {
float length = x * x + y * y + z * z;
if (length != 1f && length != 0f) {
length = (float) (1.0 / Math.sqrt(length));
return new Vector3f(x * length, y * length, z * length);
}
return new Vector3f(x, y, z);
}
/**
* 求单位向量
*/
public Vector3f normalizeLocal() {
float length = x * x + y * y + z * z;
if (length != 1f && length != 0f) {
length = (float) (1.0 / Math.sqrt(length));
x *= length;
y *= length;
z *= length;
}
return this;
}
注意,这里又用了一个技巧来提升性能。计算机中的除法比乘法昂贵得多,因此 normalize() 方法先计算了 length 的倒数,再做了三次乘法,这样可以提升计算的速度。
零向量不能被标准化。数学上是不允许的,因为这将导致除零。几何上也没有意义,因为零向量没有方向。
向量的加法和减法
向量的加法运算法则很简单:两个向量相加,将对应的分量相加即可。
/**
* 向量加法
*
* @param v
* @return
*/
public Vector3f add(Vector3f v) {
return new Vector3f(x + v.x, y + v.y, z + v.z);
}
/**
* 向量加法
* @param v
* @return
*/
public Vector3f addLocal(Vector3f v) {
x += v.x;
y += v.y;
z += v.z;
return this;
}
减法解释为负向量,a-b=a+(-b)。
/**
* 向量减法
*
* @param v
* @return
*/
public Vector3f subtract(Vector3f v) {
return new Vector3f(x - v.x, y - v.y, z - v.z);
}
/**
* 向量减法
*
* @param v
* @return
*/
public Vector3f subtractLocal(Vector3f v) {
x -= v.x;
y -= v.y;
z -= v.z;
return this;
}
应该注意以下几点:
- 向量不能与标量或维数不同的向量相加减
- 和标量乘法一样,向量加法满足交换律,但是向量减法不满足交换律。永远有 a+b=b+a,但 a-b=-(b-a),仅当a=b时,a-b=b-a。
向量a和b相加的几何解释为:平移向量,使向量a的头连接向量b的尾,接着从a的尾向b的头画一个向量。这就是向量加法的“三角形法则”。
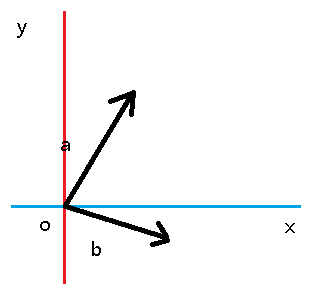
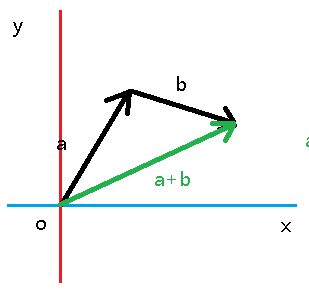
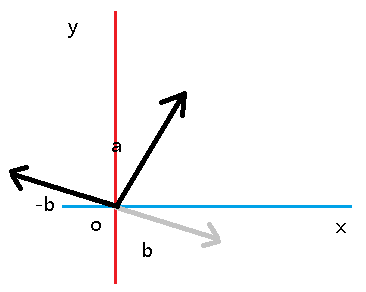
向量的减法与之类似。

一个点到另一个点的向量
计算一个点到另一个点的位移是一种非常普遍的需求,可以使用三角形法则和向量减法来解决这个问题。下图展示了怎样用a-b来计算从点B到A的位移向量。
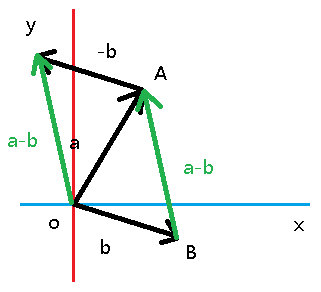
如图,将点A、B分别理解为从原点O开始的向量a、b,B到A的位移就可以用向量减法a-b来计算。
注意,减法a-b代表了从B到A的向量。简单地求“两点之间”的向量是没有意义的,因为没有指明方向。求一个点到另一个点的向量才有实际意义。
一个点到另一个点的线性插值
计算两点之间的向量很简单,如果需求改变一下,想要求两点之间某一点的向量呢?
例如:有一个物体,从起点出发向终点做匀速直线运动。走完全程需要的总时间为37秒,那么第11秒的时候这个物体运动到了什么位置?
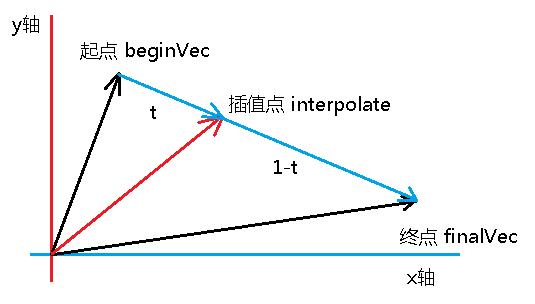
把起点和终点看作两个向量,物体其实就是在从起点到终点的向量上运动。以该向量的总长度为100%,物体已经走完的路程为 t (0~100%),可得插值点的计算公式为:
interpolate = t * (final - begin)
经过化简,这个公式可以改写为:
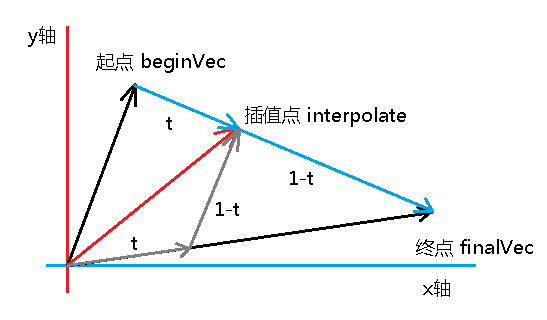
interpolate = t * final + (1 - t) * begin
这个化简公式的几何意义也很简单:过插值点作一条平行于起点向量的辅助线,与终点向量所在的边相交。从交点的位置,可以得到两个更小的向量,插值点向量正好是这两个向量的和。根据相似三角形定理,可知这两个向量分别是 t * final 和 (1 - t) * begin。
代码实现如下:
/**
* 在当前向量与final向量之间线性插值。
*
* this=(1-changeAmnt)*this + changeAmnt * finalVec
* @param finalVec 终向量
* @param changeAmnt 插值系数,取值范围为 0.0 - 1.0。
*/
public Vector3f interpolateLocal(Vector3f finalVec, float changeAmnt) {
this.x=(1-changeAmnt)*this.x + changeAmnt*finalVec.x;
this.y=(1-changeAmnt)*this.y + changeAmnt*finalVec.y;
this.z=(1-changeAmnt)*this.z + changeAmnt*finalVec.z;
return this;
}
/**
* 在当开始向量与终向量之间线性插值。
* this=(1-changeAmnt)*beginVec + changeAmnt * finalVec
* @param beginVec 开始向量(changeAmnt = 0)
* @param finalVec 终向量(changeAmnt = 1)
* @param changeAmnt 插值系数,取值范围为 0.0 - 1.0。
*/
public Vector3f interpolateLocal(Vector3f beginVec,Vector3f finalVec, float changeAmnt) {
this.x=(1-changeAmnt)*beginVec.x + changeAmnt*finalVec.x;
this.y=(1-changeAmnt)*beginVec.y + changeAmnt*finalVec.y;
this.z=(1-changeAmnt)*beginVec.z + changeAmnt*finalVec.z;
return this;
}
距离公式
距离公式用来计算两点之间的距离。从几何意义上来说,两点之间的距离等于从一个点到另一个点的向量的长度。先计算从a到b的向量d,然后再计算d的长度即可。
注意,哪个点是a和哪个点是b并不重要,因为我们只关心向量d的长度,不关心它的方向。
/**
* 求两点之间的距离
*
* @param v
* @return
*/
public float distance(Vector3f v) {
double dx = x - v.x;
double dy = y - v.y;
double dz = z - v.z;
return (float) Math.sqrt(dx * dx + dy * dy + dz * dz);
}
/**
* 求两点之间距离的平方
*
* @param v
* @return
*/
public float distanceSquared(Vector3f v) {
double dx = x - v.x;
double dy = y - v.y;
double dz = z - v.z;
return (float) (dx * dx + dy * dy + dz * dz);
}
向量点乘
向量的点乘也称作内积。向量点乘就是对应分量乘积的和,其结果是一个标量。
/**
* 向量点乘(内积)
*
* @param v
* @return
*/
public float dot(Vector3f v) {
return x * v.x + y * v.y + z * v.z;
}
点乘等于向量长度与向量夹角的cos值的积。
a dot b = |a|*|b|*cos(θ)
这个公式很有用,如果a、b都是单位向量,点乘就可以直接算出它们之间的 cos 值。根据cos值,即可以计算两个向量之间的夹角:
- 若 cos > 0。说明a和b的夹角 0° <= θ < 90°;
- 若 cos = 0,说明a和b正交(垂直),即 θ ≈ 90°;
- 若 cos < 0,说明a和b的夹角 90° < θ <= 180°。
向量的大小并不影响点乘结果的符号,所以根据cos的符号就可以判断a和b的大致方向。
向量之间的夹角
利用点乘,很容易求得两个单位向量间的夹角。
/**
* 求两个向量之间的夹角(弧度制)
* 注意:参与运算的两个向量都应该是单位向量
*
* @param v
* @return
*/
public float angleBetween(Vector3f v) {
float dotProduct = x * v.x + y * v.y + z * v.z;
float angle = (float) Math.acos(dotProduct);
return angle;
}
向量投影
已知两个向量a、b,可以把a分解成两个向量,一个垂直于b,另一个平行于b。平行于b的那个向量称为a在b上的投影。
根据向量点乘公式,易得两个向量夹角的 cos 值,根据 cos 值可以进一步求得向量的投影。
/**
* 向量投影
*
* @param v
* @return 返回一个新的向量,它平行于另一个向量。
*/
public Vector3f project(Vector3f v){
float n = x * v.x + y * v.y + z * v.z; // A . B
float d = v.lengthSquared(); // |B|^2
float scalor = n / d;
return new Vector3f(v.x * scalor, v.y * scalor, v.z * scalor);
}
/**
* 向量投影
* @param v
* @return 返回一个新的向量,它平行于另一个向量。
*/
public Vector3f projectLocal(Vector3f v){
float n = this.dot(v); // A . B
float d = v.lengthSquared(); // |B|^2
float scalor = n / d;
x = v.x * scalor;
y = v.y * scalor;
z = v.z * scalor;
return this;
}
向量叉乘
叉乘将会得到一个新的向量,它垂直于原来的两个向量,其长度 |a×b| 正好是以向量a、b位两边的平行四边形的面积。叉乘的这种特性,经常用于求三角形的表面法线。
/**
* 向量叉乘(外积)
*
* @param v
* @return 返回一个新的向量,它垂直于当前两个向量。
*/
public Vector3f cross(Vector3f v) {
float rx = y * v.z - z * v.y;
float ry = z * v.x - x * v.z;
float rz = x * v.y - y * v.x;
return new Vector3f(rx, ry, rz);
}
/**
* 向量叉乘(外积)
*
* @param v
* @return 返回一个新的向量,它垂直于当前两个向量。
*/
public Vector3f crossLocal(Vector3f v) {
float tempX = y * v.z - z * v.y;
float tempY = z * v.x - x * v.z;
z = x * v.y - y * v.x;
x = tempX;
y = tempY;
return this;
}
已知 a×b 垂直于a、b。但是垂直于a、b又两个方向。a×b指向哪个方向呢?通过将a的头与b的尾相接,并检查从a到b是顺时针还是逆时针,能够确定a×b的方向。
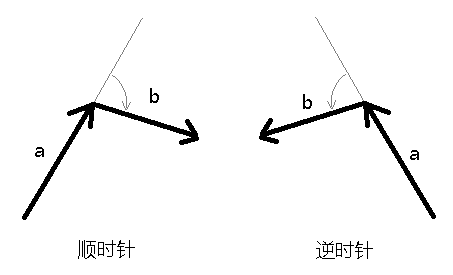
在右手坐标系中,如果a和b呈逆时针,则a×b指向您;如果a和b呈顺时针,则a×b远离您。
在左手坐标系中,则正好相反。如果a和b呈逆时针,则a×b远离您;如果a和b呈顺时针,则a×b指向您。
我们可以用右手来辅助记忆。将右手握拳,伸出大拇指指向自己,此时其他四指正好是逆时针方向,大拇指的方向就是a×b的方向。
现在你明白什么叫右手坐标系了吧。:)
向量的乘法
除点乘和叉乘外,还有另一种乘法,计算方法是直接将向量的分量相乘,它的几何意义是把向量按比例放大(缩小)。
/**
* 向量乘法
*
* @param v
* @return
*/
public Vector3f mult(Vector3f v) {
return new Vector3f(x * v.x, y * v.y, z * v.z);
}
/**
* 向量乘法
*
* @param v
* @return
*/
public Vector3f multLocal(Vector3f v) {
x *= v.x;
y *= v.y;
z *= v.z;
return this;
}
向量的除法
向量的除法并没有太大的意义,可以用乘法来代替实现。不过有时为了简化计算工作,也会定义除法的规则。
向量除以标量,等于向量乘以这个标量的倒数:v / s = v * 1/s。
/**
* 标量除法
* @param scalor
* @return
*/
public Vector3f divide(float scalor) {
scalor = 1 / scalor;
return new Vector3f(x * scalor, y * scalor, z * scalor);
}
/**
* 标量除法
* @param scalor
* @return
*/
public Vector3f divideLocal(float scalor) {
scalor = 1 / scalor;
x *= scalor;
y *= scalor;
z *= scalor;
return this;
}
向量a除以b,直接将各分量相除即可。
/**
* 向量除法
* @param v
* @return
*/
public Vector3f divide(Vector3f v) {
return new Vector3f( x / v.x, y / v.y, z / v.z);
}
/**
* 向量除法
* @param v
* @return
*/
public Vector3f divideLocal(Vector3f v) {
x /= v.x;
y /= v.y;
z /= v.z;
return this;
}
注意,我没有在方法内做任何校验,但在做除法运算时应该要确保分母不为0。
总结
本章实现了三维向量的定义和各种运算。很多三维向量运算都可以推导到其他维度,比如二维向量和四维向量。
二维向量叉乘
比较特别的是,二维向量叉乘的结果是一个三维向量,它垂直于二维向量所在的平面。可以把二维向量当做是z分量为0的向量,然后计算叉乘:
(x1, y1, 0) cross (x2, y2, 0) = (0, 0, x1 * y2 - y1 * x2)
按照右手定则,如果向量v1和v2的方向为逆时针,叉乘向量就指向正方向。如果v1和v2的方向为顺时针,叉乘向量就指向负方向。根据 x1 * y2 - y1 * x2 的值,就可以判断向量v1和v2的方向。

在右手坐标系中,如果这个值大于0,说明v1和v2呈逆时针方向。换句话说,点v2位于向量v1的左侧。若值小于0,则说明点v2位于向量v1的右侧;当这个值为0时,说明向量 v1 和 v2 共线。
这个性质,在 Vector2f 类中用于判断向量的相对位置。
/**
* 判别式
*/
public float determinant(Vector2f v) {
return (x * v.y) - (y * v.x);
}
public Vector3f cross(Vector2f v) {
return new Vector3f(0, 0, determinant(v));
}
四维向量初始化
在定义Vector4f时,我学习 Shader 语言中的用法,允许使用三维向量、二维向量来初始化四维向量。
/**
* 使用一个三维向量+一个标量来构造四维向量。
* @param v
* @param w
*/
public Vector4f(Vector3f v, float w) {
this.x = v.x;
this.y = v.y;
this.z = v.z;
this.w = w;
}
/**
* 使用2个二维向量来构造四维向量。
* @param v0
* @param v1
*/
public Vector4f(Vector2f v0, Vector2f v1) {
this.x = v0.x;
this.y = v0.y;
this.z = v1.x;
this.w = v1.y;
}
虽然不知道有什么用,但也许将来模拟着色器的时候用得着吧。